JS算法-堆和排序
堆stack简介
二叉堆 binary heap
二叉堆是一颗完全二叉树
堆分为两种:
-
最大堆:堆中某个节点的值总是不大于其父节点的值
-
最小堆
以下都以最大堆讲解。
堆stack复杂度
-
时间复杂度:O(nlog2n)
-
空间复杂度: O(1)
-
稳定性:不稳定
堆的基本存储-heapstorage
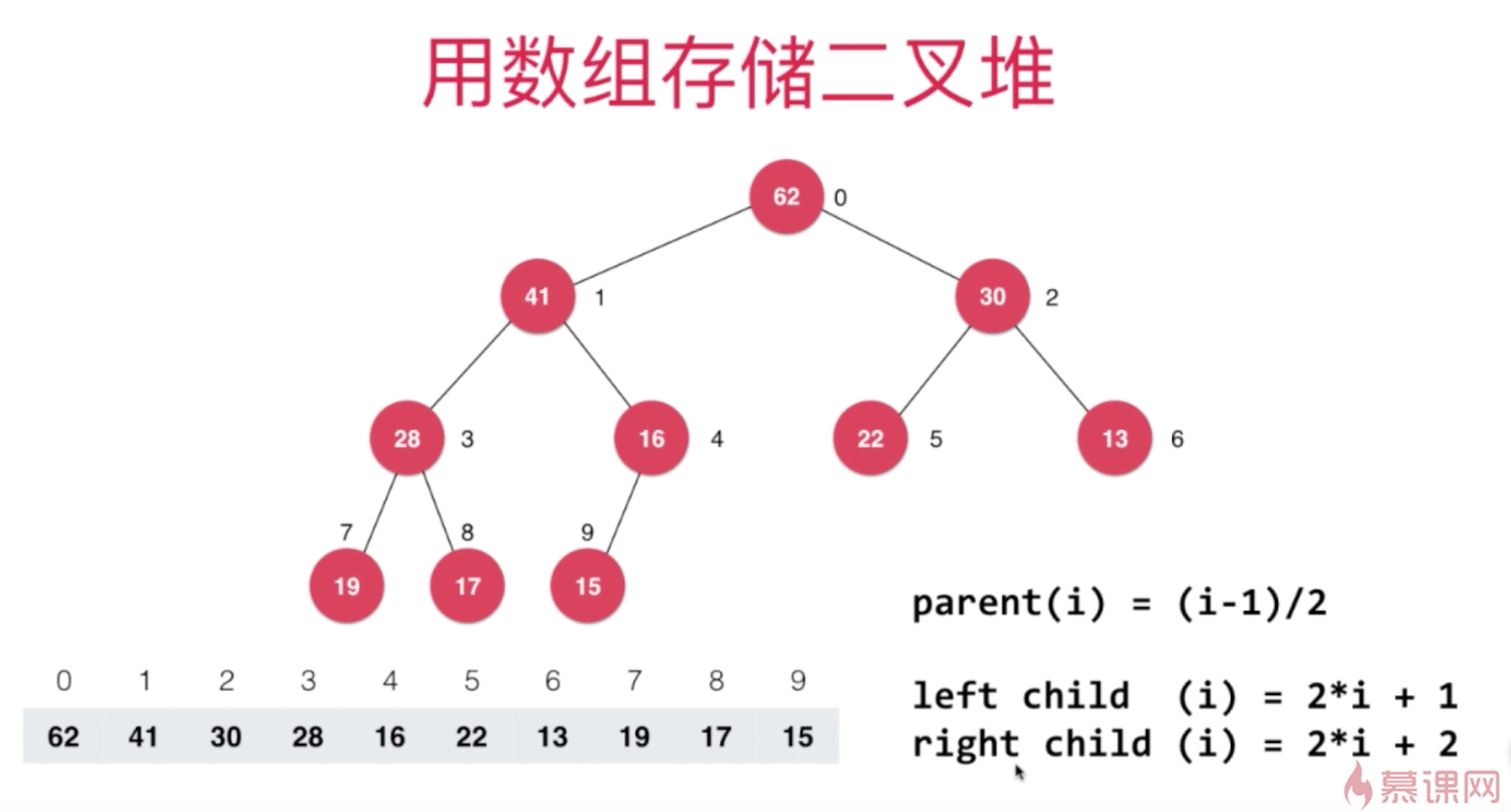
用数组存储二叉堆
Shift Up 入队
插入一个随机数后,重新排列最大二叉堆的顺序
做法:
(1)插入的数放入数组追加到最后,
(2)插入的数对比它父节点上的数,若比父节点大,两个交换,
(3)重复(2),直到插入的数比父节点小。
function shiftUp(k) {
while(k > 1 && arr[k/2] < arr[k]) {
swap( arr[k/2] , arr[k]);
k/2;
}
}
Shift Down 出队
做法:
(1)把堆最后一个位置上的数A,挪到要删除元素的位置上。做 shiftDown()位置变换,使堆最后那个数A找到它该待的位置。
(2)数A与两个子节点比较大小,若比子节点小,那么它与更大的那个子节点交换位置(使换位后父节点比两个子节点都大)
(3)重复(2)直到数A比两个子节点都大
索引从1开始
function shiftDown(k) {
while(2*k <= count) {
var j = 2*k;
if(j + 1 <= count && data[j+1] > data[j]) {
j += 1;
}
if (data[k] >= data[j]) {
break;
}
swap(data[k] , data[j]);
k = j;
}
}
构建一个最大堆-Heapify
Heapify过程
(1)将一个数组的内容逐一放入堆中;
(2)从第一个不是叶子节点的数(索引为k=n/2),向上(直到k=1)依次做shiftDown(k)
/* 将最大的元素调整到堆顶 */
/* pos为从当前位置向下遍历所有子节点,len为需要考虑的arr形成大堆顶的长度 */
function AdjustHeap(arr, pos, len){ // 从索引0开始
while(pos * 2 + 1 < len){ //递归遍历所有的子节点
var child = pos * 2 + 1; //定位到当前节点的左边的子节点
//判断当前节点是否有右节点,若右节点较大,就采用右节点和当前节点进行比较
if(child + 1 < len && arr[child] < arr[child + 1]){
child += 1;
}
if (arr[pos] >= arr[child]) {
break;
}
//比较当前节点和最大的子节点,当前子节点小于最大子节点就交换,交换后将当前节点定位到子节点上
swap(arr, pos, child);
pos = child; // 交换到子节点child上的父元素可能会影响到child自身的子节点,继续交换,直到生成大堆顶
}
}
// 交换arr[i]与arr[j]
function swap(arr,i,j){
var temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
堆排序-heap sort
堆排序:原理是,将数组看成一个完全二叉树;
形如:
0
/ \
1 2
/ \ / \
3 4 5 6
/ \ /
7 8 9
(1)只需要遍历一半的值,进行循环比对,把最大的节点赋值到根的位置,然后把根部的值和最后一个数值交换,排除最后一个数值
(2)继续打造大顶堆,最终形成一个小顶堆的算法!
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>test</title>
</head>
<body>
<script>
// function AdjustHeap(arr, pos, len){
// var swap = arr[pos]; //保存当前节点
// var child = pos * 2 + 1; //定位到当前节点的左边的子节点
// while(child < len){ //递归遍历所有的子节点
// //判断当前节点是否有右节点,若右节点较大,就采用右节点和当前节点进行比较
// if(child + 1 < len && arr[child] < arr[child + 1]){
// child += 1;
// }
// //比较当前节点和最大的子节点,小于就交换,交换后将当前节点定位到子节点上
// if(arr[pos] < arr[child]){
// arr[pos] = arr[child];
// pos = child;
// child = pos * 2 + 1;
// }
// else{
// break;
// }
// arr[pos] = swap;
// }
// }
/* 将最大的元素调整到堆顶 */
/* pos为从当前位置向下遍历所有子节点,len为需要考虑的arr形成大堆顶的长度 */
function AdjustHeap(arr, pos, len){
while(pos * 2 + 1 < len){ //递归遍历所有的子节点
var child = pos * 2 + 1; //定位到当前节点的左边的子节点
//判断当前节点是否有右节点,若右节点较大,就采用右节点和当前节点进行比较
if(child + 1 < len && arr[child] < arr[child + 1]){
child += 1;
}
if (arr[pos] >= arr[child]) {
break;
}
//比较当前节点和最大的子节点,当前子节点小于最大子节点就交换,交换后将当前节点定位到子节点上
swap(arr, pos, child);
pos = child; // 交换到子节点child上的父元素可能会影响到child自身的子节点,继续交换,直到生成大堆顶
}
}
/* 构建堆:
* 满足:树中任一非叶子结点的关键字均不大于(或不小于)其左右孩子结点的关键字。
* 实现:从最后一个拥有子节点的节点开始,将该节点和其他节点进行比较,将最大的数交换给该节点,
* 交换后再依次向前节点进行相同的交换处理,直到构建出大顶堆。
*/
function BuildHeap(arr){
for(var i = arr.length/2; i >= 0; i--){ //首先构造一个标准的大堆顶,只需要便利二叉树一半的节点,就能够把大堆顶构造出来
AdjustHeap(arr, i, arr.length);
}
}
/*堆排序算法*/
function HeapSort(arr){
BuildHeap(arr); //构造大堆顶
for(var i=arr.length-1; i>0; i--){ //从数组的尾部进行调整
swap(arr, i, 0); //堆顶永远是最大的元素,将堆顶和尾部元素交换,最大元素就保存在尾部,并且不参与后面的调整
AdjustHeap(arr, 0, i); //排除最后一个元素,将前面剩下的所有元素继续进行大堆顶,将最大的元素调整到堆顶
}
}
// 交换arr[i]与arr[j]
function swap(arr,i,j){
var temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
var arr = [46,12,33,72,68,19,80,33];
console.log('before: ' + arr);
HeapSort(arr);
console.log(' after: ' + arr);
</script>
</body>
</html>
堆排序-法二
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>test</title>
</head>
<body>
<script>
var arr = [8, 6, 2, 3, 1, 5, 7, 4];
function HeapAdjust(arr,s,m){ //使用调整大顶堆进行排序,将s到m之间的数值调整为大顶堆!
var temp=arr[s]; //将大顶堆顶值负值给temp;
for(var j = 2*s+1; j < m; j = 2*j+1) //由于下标是0;这里只从0,1,3,5...每列的第一个数字开始便利就行
{
if(j < m && arr[j] < arr[j+1]) //如果当前下标的值比下一个下标的数值比下一个小(我们是要找最大的那个),则就使j+1指向那个数字
++j;
if(temp >= arr[j]) //如果堆顶的值大于当前j下标的值,就不用再找了。跳出循环
break;
arr[s] = arr[j]; //小于j下标的值,就把arr[j]复制给arr[s]
s = j; //s就指向当前j的位置,为下步把顶值赋值到这个位置做准备(循环完之前,先不赋值)
}
arr[s] = temp; //最后赋值给arr[s](s指向现在找到的最大的大堆顶的值)
}
function HeapSort(arr){
for(var i = arr.length/2; i >= 0; i--) //首先构造一个标准的大堆顶,只需要遍历二叉树一半的节点,就能够把大堆顶构造出来
HeapAdjust(arr, i, arr.length);
for(var i = arr.length; i > 0; i--){ //构造完之后 把堆顶的值和最后一个互换,然后 排除最后一个继续进行打造大堆顶!
swap(arr,0,i-1);
HeapAdjust(arr,0,i-2);
}
}
function swap(arr,i,j){
var temp=arr[i];
arr[i]=arr[j];
arr[j]=temp;
}
HeapSort(arr)
console.log(arr);
</script>
</body>
</html>

