JS算法-二叉搜索树(BST)
二叉搜索树(BST)简介
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树:
-
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
-
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
-
它的左、右子树也分别为二叉排序树。
二分搜索树不一定是完全二叉树
二叉搜索树的基本操作和树的高度成正比,所以如果是一棵完全二叉树的话最坏运行时间为Θ(lgn),但是若是一个n个节点连接成的线性树,那么最坏运行时间是Θ(n)。
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>test</title>
</head>
<body>
<script>
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
function show() {
return this.data;
}
function BST() {
this.root = null;
}
console.log();
</script>
</body>
</html>
二分搜索树的节点插入-insert
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>test</title>
</head>
<body>
<script>
function Node(data, left, right) {
this.data = data;
this.left = left;
this.right = right;
this.show = show;
}
function show() {
return this.data;
}
function BST() {
this.root = null;
this.insert = insert;
}
function insert(data) {
var node = new Node(data, null, null);
if (this.root === null); {
this.root === node;
} else {
var curNode = this.root;
var parent;
while(true) {
parent = curNode;
if (data < curNode.data) {
curNode = curNode.left;
if (curNode === null) {
parent.left = node;
break;
}
} else {
curNode = curNode.right;
if (curNode === null) {
parent.right = node;
break;
}
}
}
}
}
</script>
</body>
</html>
二分搜索树的查找-find
function find(data) {
var curNode = this.root;
while (curNode !== null) {
if (curNode.data === data) {
return curNode;
}
else if (curNode.data > data) {
curNode = curNode.right;
}
else {
curNode = curNode.left;
}
}
return null;
}
查找最大最小值-getMax
//取最大值
function getMax = function(){
var currNode = this.root;
while(currNode.right != null){
currNode = currNode.right;
}
return currNode.data;
}
//取最小值
function getMin = function(){
var currNode = this.root;
while(currNode.left != null){
currNode = currNode.left;
}
return currNode.data;
}
二分搜索树的遍历-traversal
(深度优先遍历)

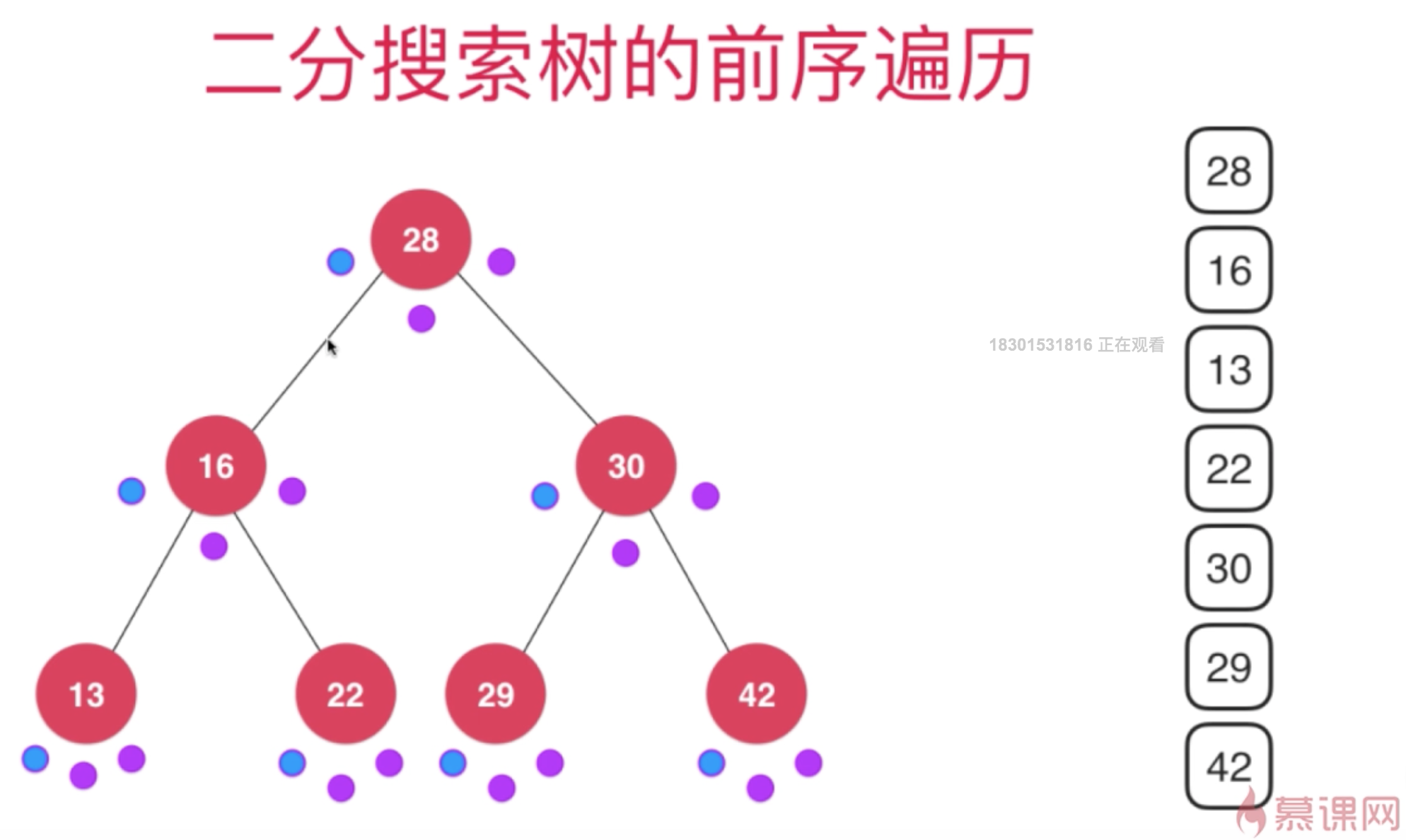
//前序遍历
function preOrder(node) {
if (node !== null) {
console.log(node.data);
this.preOrder(node.left);
this.preOrder(node.right);
}
}
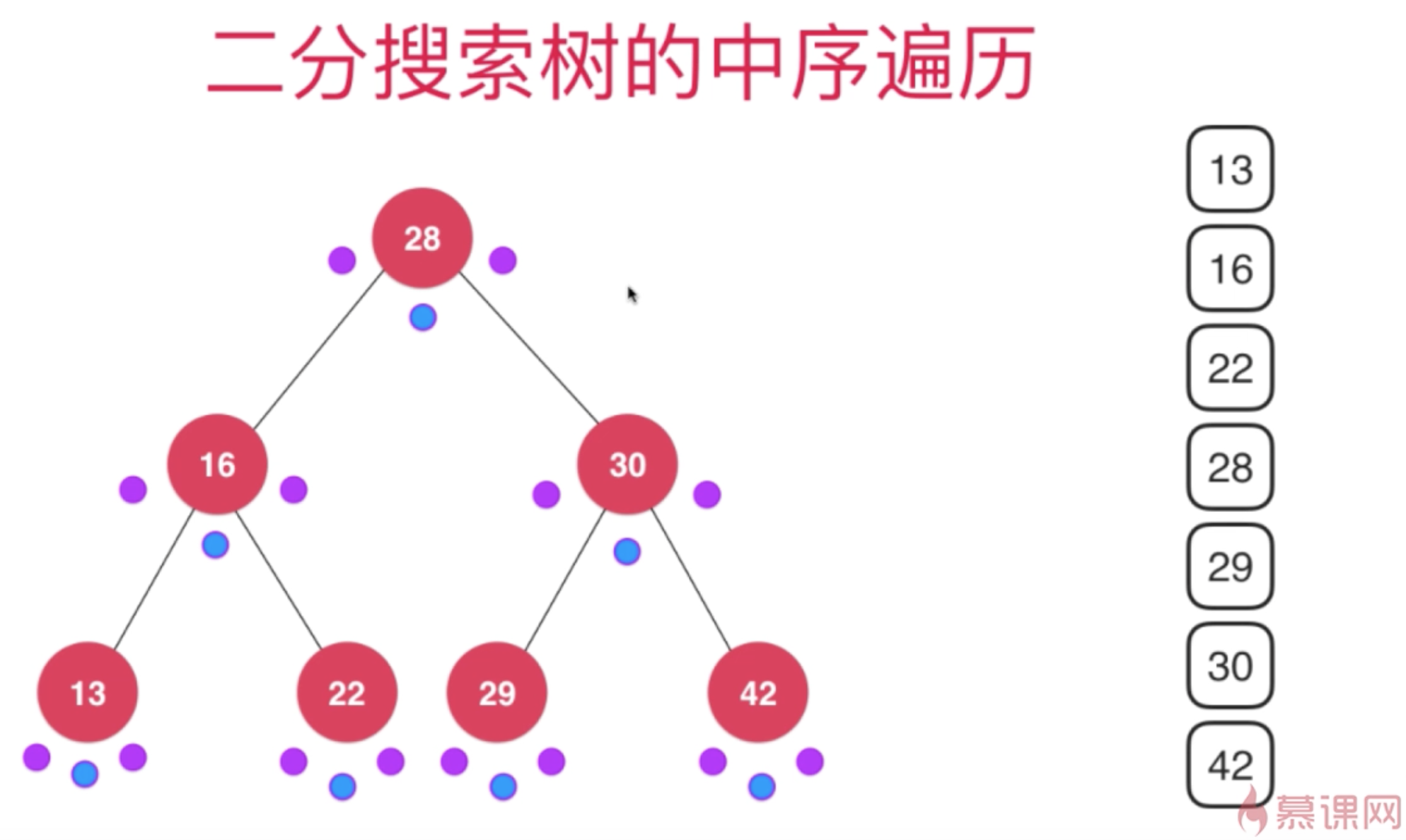
//中序遍历
function inOrder = function(node){
if(node != null){
this.inOrder(node.left);
console.log(node.data);
this.inOrder(node.right);
}
}
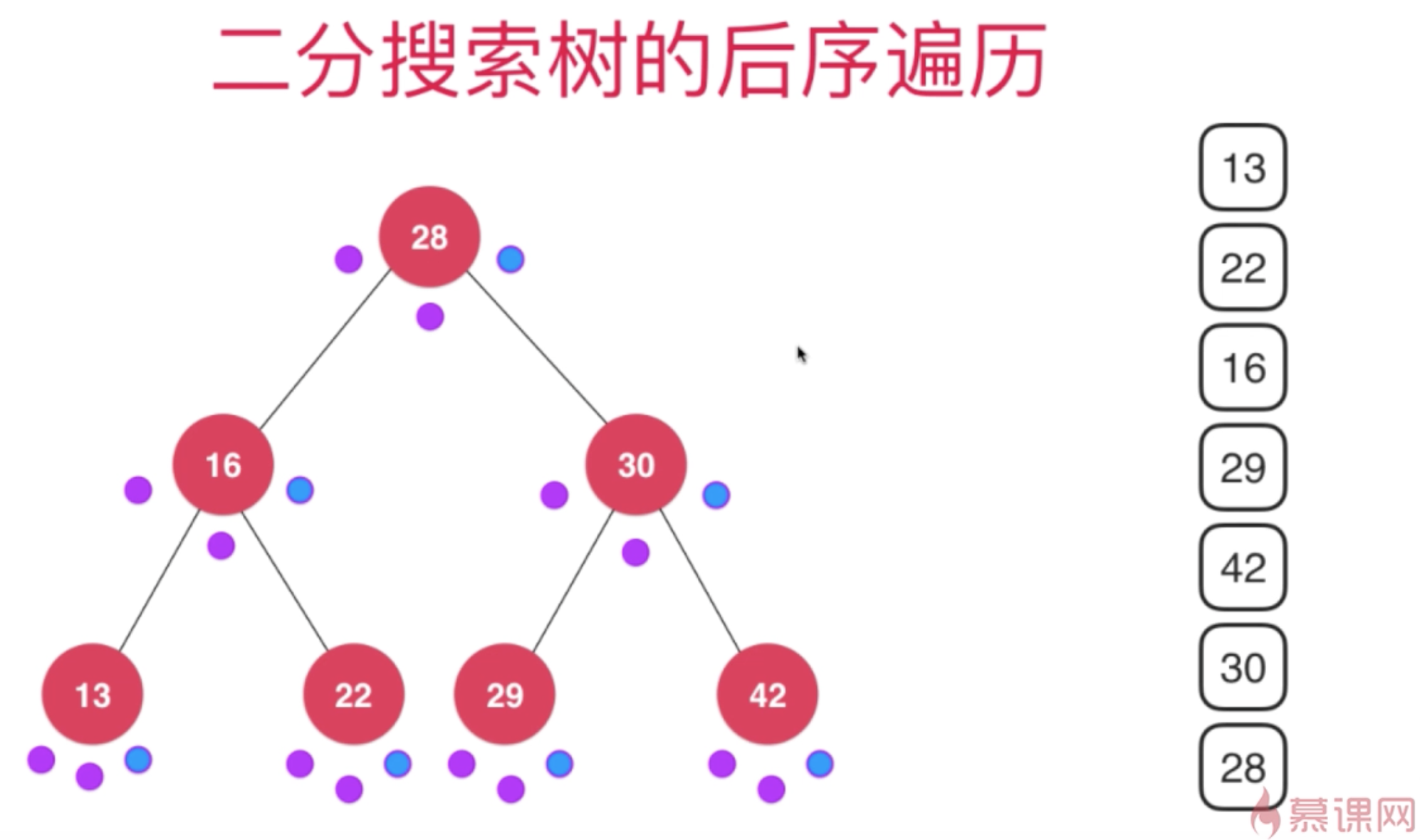
//后序遍历
function postOrder = function(node){
if(node != null){
this.postOrder(node.left);
this.postOrder(node.right);
console.log(node.data);
}
}
二分搜索树节点的删除-Deletion
function remove(data) {
root = removeNode(this.root, data);
}
function removeNode(node, data) {
if (node == null) {
return null;
}
if (data == node.data) {
// 没有子节点的节点
if (node.left == null && node.right == null) {
return null;
}
// 没有左子节点的节点
if (node.left == null) {
return node.right;
}
// 没有右子节点的节点
if (node.right == null) {
return node.left;
}
// 有两个子节点的节点
var tempNode = getSmallest(node.right);
node.data = tempNode.data;
node.right = removeNode(node.right, tempNode.data); return node;
}
else if (data < node.data) {
node.left = removeNode(node.left, data);
return node;
}
else {
node.right = removeNode(node.right, data);
return node;
}
}
二分搜索树完整代码-all
BSTNode.js
(function(){
"use strict";
function Node(data, left, right){
this.data = data;
this.left = left;
this.right = right;
}
module.exports = Node;
})();
BSTree.js
(function(){
"use strict";
var Node = require("./lib/BSTNode");
function BSTree(){
this.root = null;
}
BSTree.prototype.remove = function(data){
if(this.root == null)
return false;
var currNode = this.root;
var parent = null;
//注意边界值,如果被删除的是根结点,循环是不进入的,parent为null
while(currNode != null && currNode.data != data) {
parent = currNode;
if(data < currNode.data){
currNode = currNode.left;
}else{
currNode = currNode.right;
}
}
if(currNode == null){
return false;
}
if(currNode.left == null || currNode.right == null){ //至少有一个孩子为空时
if(parent == null){ //处理边界值,但左右子树同时存在时,不会出问题
this.root = currNode.left == null ? currNode.right : currNode.left;
}
else if(parent.left == currNode){
parent.left = currNode.left == null ? currNode.right : currNode.left;
}
else{
parent.right = currNode.left == null ? currNode.right : currNode.left;
}
}else{ //孩子都不为空,找直接后继
var mid = currNode.right;
parent = currNode;
while(mid.left != null){
parent = mid;
mid = mid.left;
}
currNode.data = mid.data; //后继取代被删节点
if(parent.left == mid){ //删除其后继
parent.left = mid.right;
}
else{
parent.right = mid.right;
}
}
return true;
};
BSTree.prototype.find = function(data){
var currNode = this.root;
while(currNode != null){
if(currNode.data == data){
return currNode;
}
else if(data < currNode.data){
currNode = currNode.left;
}
else{
currNode = currNode.right;
}
}
return null;
};
//取最小值
BSTree.prototype.getMin = function(){
var currNode = this.root;
while(currNode.left != null){
currNode = currNode.left;
}
return currNode.data;
};
//取最大值
BSTree.prototype.getMax = function(){
var currNode = this.root;
while(currNode.right != null){
currNode = currNode.right;
}
return currNode.data;
};
//后序遍历
BSTree.prototype.postOrder = function(node){
if(node != null){
this.postOrder(node.left);
this.postOrder(node.right);
console.log(node.data);
}
};
//前序遍历
BSTree.prototype.preOrder = function(node){
if(node != null){
console.log(node.data);
this.preOrder(node.left);
this.preOrder(node.right);
}
};
//中序遍历
BSTree.prototype.inOrder = function(node){
if(node != null){
this.inOrder(node.left);
console.log(node.data);
this.inOrder(node.right);
}
};
BSTree.prototype.insert = function(data){
var node = new Node(data, null, null);
if(this.root == null){
this.root = node;
}
else{
var currNode = this.root;
var parent; //因为没有父指针,需要存储当前节点的父节点
while(true){
parent = currNode;
if(data < currNode.data){
currNode = currNode.left;
if(currNode == null){
parent.left = node;
break;
}
}
else{
currNode = currNode.right;
if(currNode == null){
parent.right = node;
break;
}
}
}
}
};
module.exports = BSTree;
})();

