JS算法-图的基础
图的基础-graph
图和散列表、二叉树一样,是一种非线性数据结构。
图由一系列顶点以及连接顶点的边构成。
如果图中每两个顶点之间都有路径相连,则称该图是连通的。
图的分类-classification
㈠
无向图
有向图
㈡
有权图
无权图
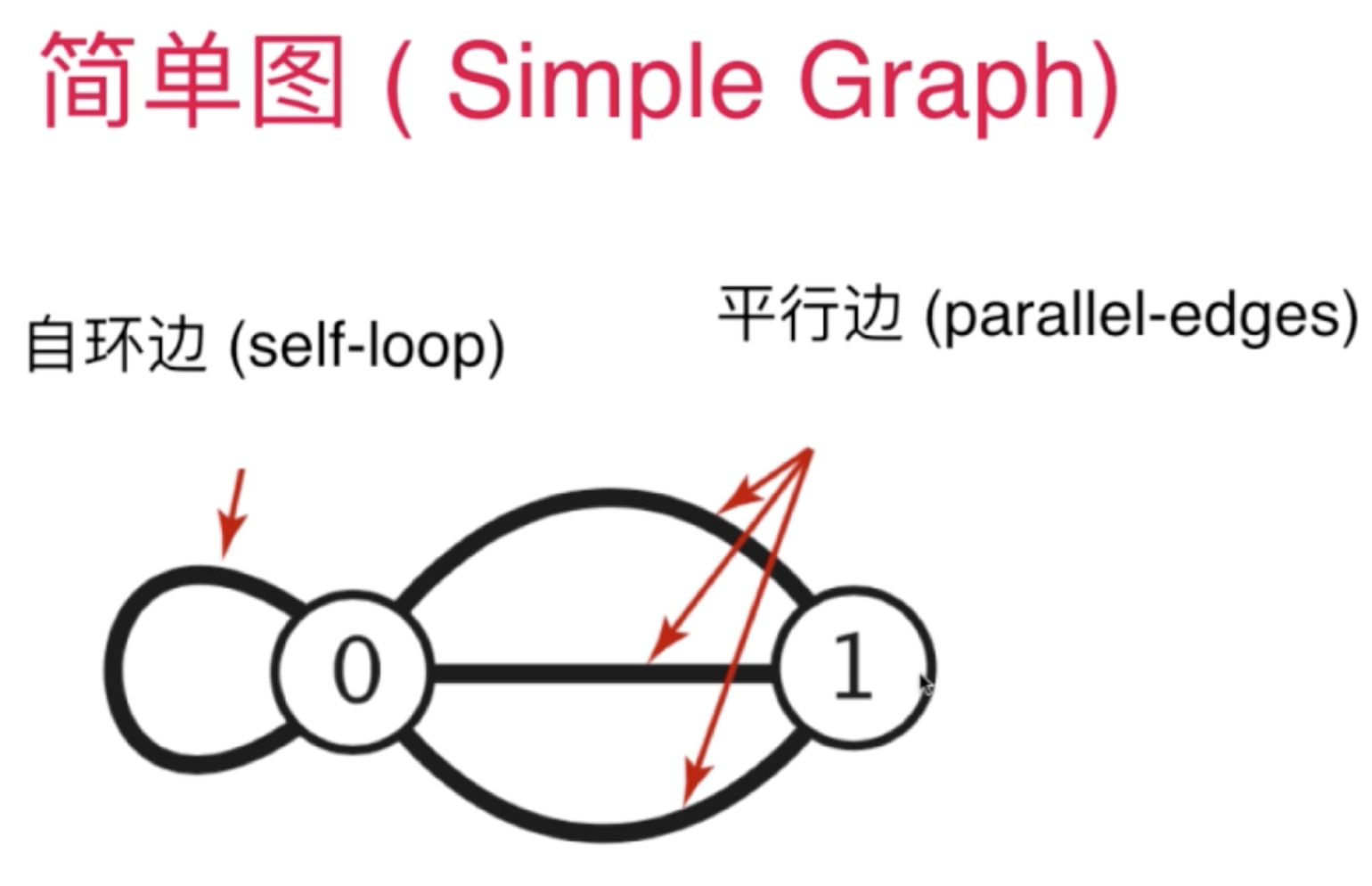
图的表示-representation
- 邻接表:适合表示稀疏图
- 邻接矩阵:适合表示稠密图
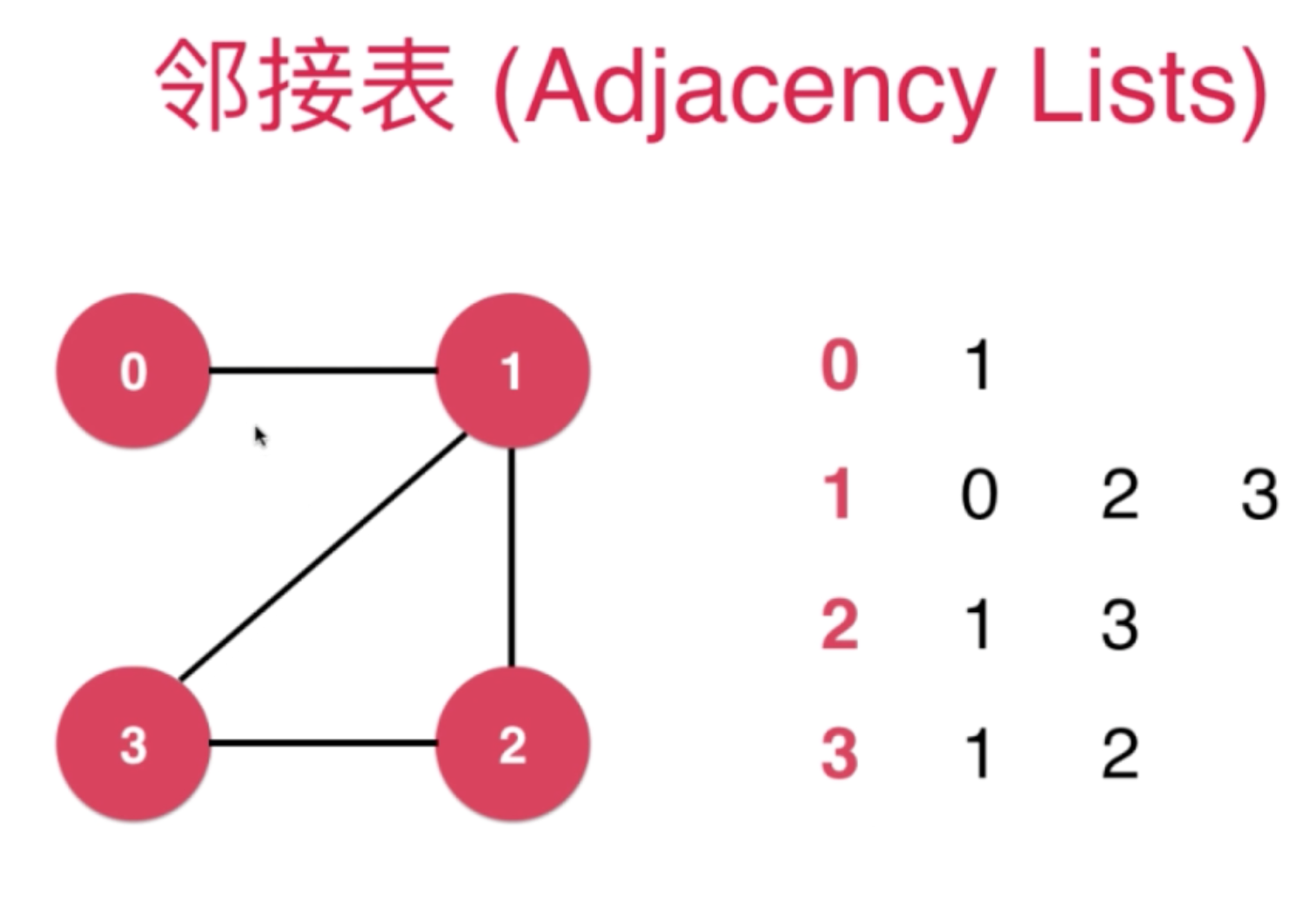
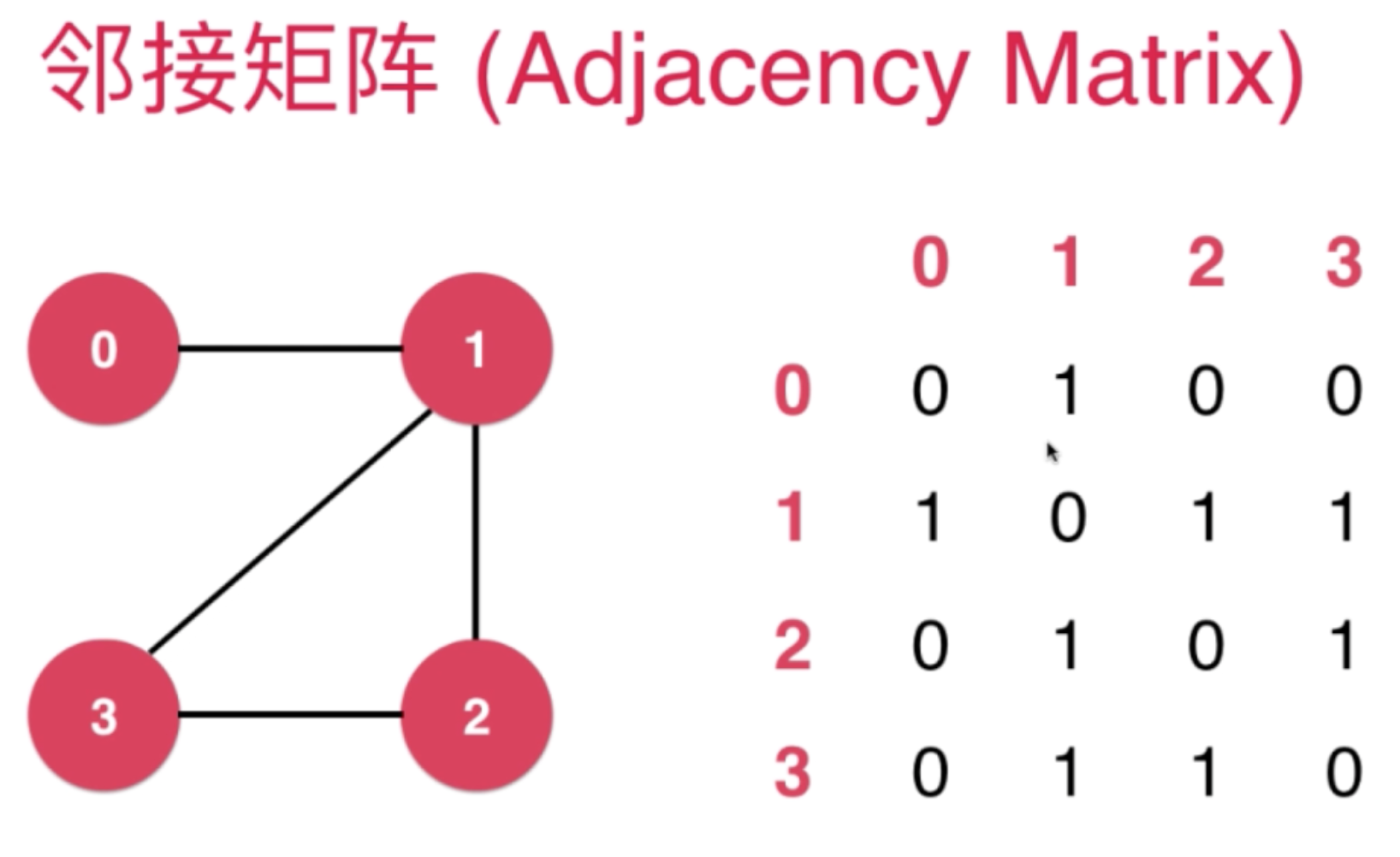
邻接表-Adjacency list
邻接表-表示无向图
创建图类
function Graph(v){
this.vertices = v;
this.edges = 0;
this.adj = [];
for(var i = 0; i<this.vertices;i++){
this.adj[i] = [];
}
this.addEdge = addEdge; // 添加边
this.toString = toString;
this.showGraph = showGraph; // 遍历
//记录已经访问过的顶点
this.marked = [];
for(var i = 0;i < this.vertices;i++){
this.marked[i] = false;
}
this.dfs = dfs; // 深度优先搜索
this.bfs = bfs; // 广度优先搜索
}
添加边
function addEdge(v,w){
this.adj[v].push(w);
this.adj[w].push(v);
this.edges++;
}
遍历
function showGraph(){
for(var i =0;i < this.vertices;i++){
for(var j = 0;j < this.vertices;j++){
if(this.adj[i][j] != undefined){
console.log(i+"->"+this.adj[i][j])
}
}
}
}
图的遍历-Traversal
- 深度优先搜索(Depth-First Search,DFS)
- 广度优先搜索(Breadth-First Search,BFS)
深度优先搜索-DFS
图的深度优先遍历 - 复杂度
- 稀疏图-邻接表:O(V + E)
- 稠密图-邻接矩阵:O(V^2)
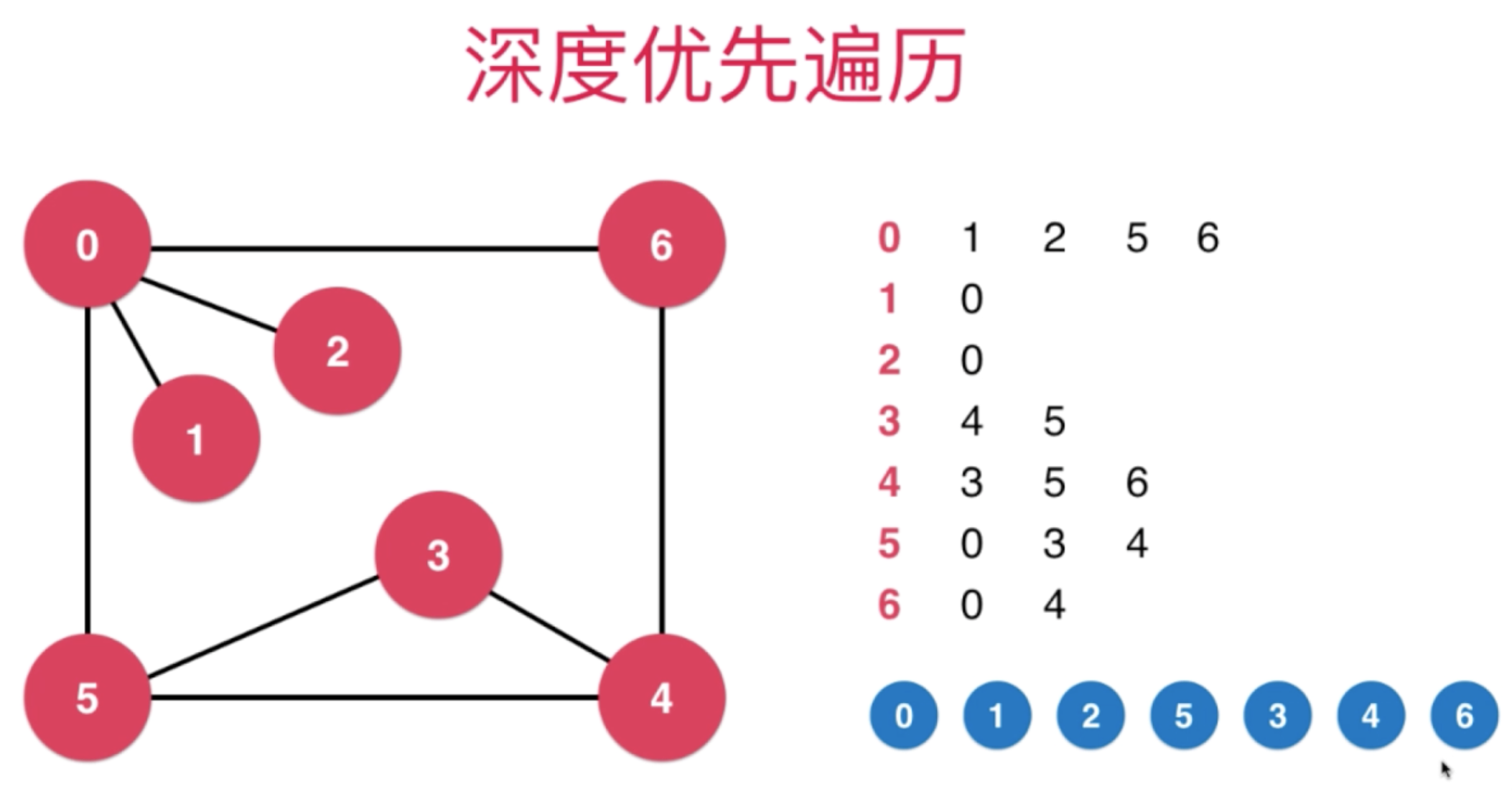
//深度优先搜索
function dfs(v){
this.marked[v] = true;
//输出一下
if(this.adj[v] != undefined){
document.write("<br/>已访问:" + v);
}
for(var i = 0;i<this.adj[v].length;i++){
var w = this.adj[v][i];
if(!this.marked[w]){
this.dfs(w);
}
}
}
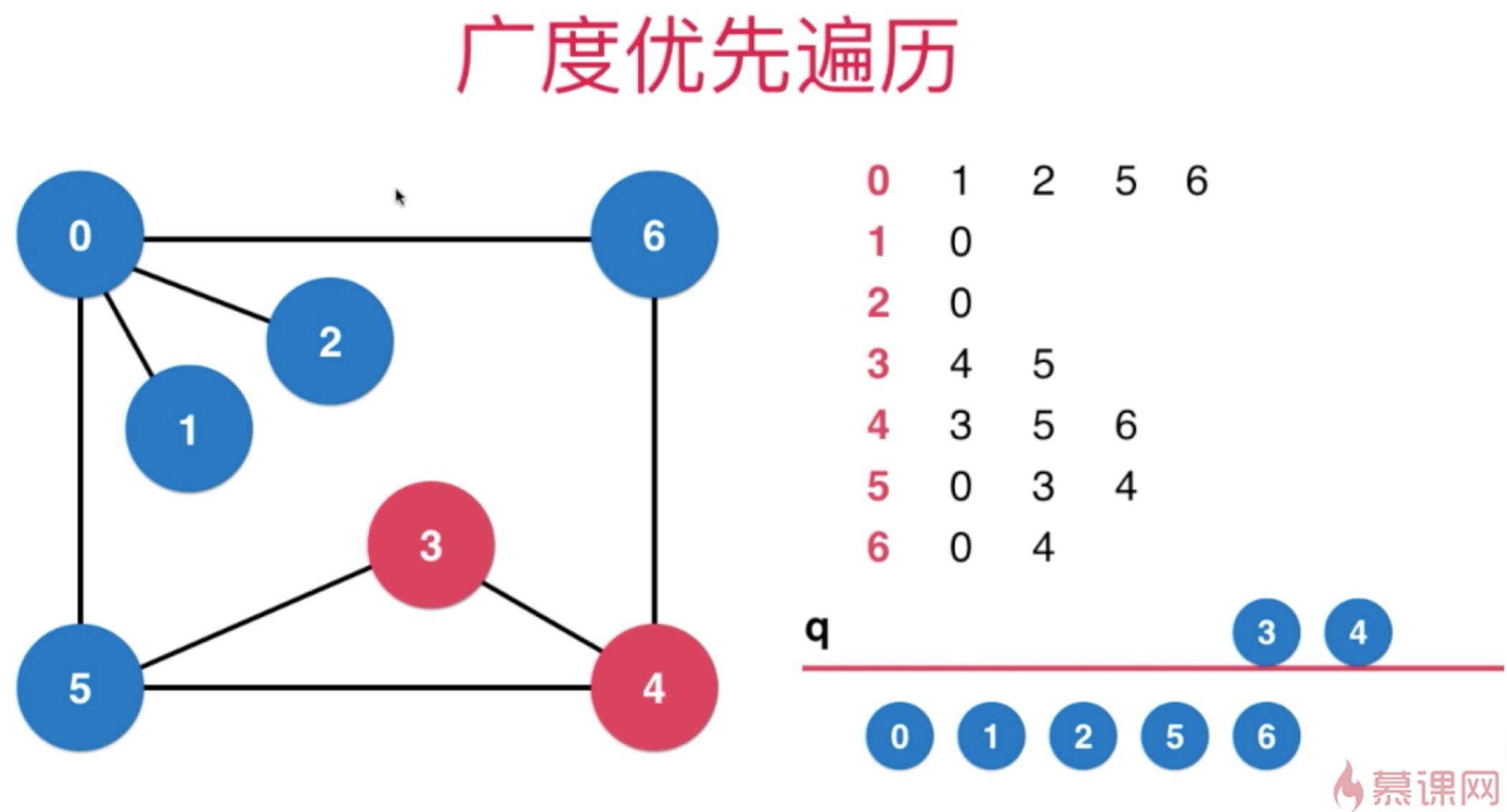
广度优先搜索-BFS
广度优先遍历求出了无权图的最短路径
//广度优先
function bfs(s){
var queue = [];
this.marked[s] = true;
queue.push(s);
while(queue.length > 0){
var v = queue.shift();
if(v != undefined){
console.log("已访问 :"+v);
}
for(var k in this.adj[v]){
var w = this.adj[v][k];
if(!this.marked[w]){
this.marked[w] = true;
queue.push(w);
}
}
}
}
完整demo
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8">
<title>Graph</title>
</head>
<body>
<script>
function Graph(v){
this.vertices=v;
this.edges=0;
this.adj=[];
for(var i=0;i<this.vertices;++i){
this.adj[i]=[];
}
this.addEdge=addEdge;
this.showGraph=showGraph;
//深度优先搜索
this.dfs=dfs;
this.marked=[];
for(var i=0;i<this.vertices;++i){
this.marked[i]=false;
}
// 广度搜索
this.bfs=bfs;
}
// 增加顶点
function addEdge(v,w){
this.adj[v].push(w);
this.adj[w].push(v);
this.edges++;
}
//遍历
function showGraph(){
for(var i=0;i<this.vertices;++i){
document.write('<br/>');
document.write(i+"-->");
for(var j=0;j<this.vertices;++j){
if(this.adj[i][j]!=undefined){
document.write(this.adj[i][j]+' ');
}
}
}
}
//深度优先搜索
function dfs(v){
this.marked[v] = true;
//输出一下
if(this.adj[v] != undefined){
document.write("<br/>已访问:" + v);
}
for(var i = 0;i<this.adj[v].length;i++){
var w = this.adj[v][i];
if(!this.marked[w]){
this.dfs(w);
}
}
}
//广度优先
function bfs(s){
var queue = [];
this.marked[s] = true;
queue.push(s);
while(queue.length > 0){
var v = queue.shift();
if(v != undefined){
document.write("<br/>已访问 :"+v);
}
for(var k in this.adj[v]){
var w = this.adj[v][k];
if(!this.marked[w]){
this.marked[w] = true;
queue.push(w);
}
}
}
}
//测试
var graph=new Graph(5);
graph.addEdge(0,1);
graph.addEdge(0,2);
graph.addEdge(1,3);
graph.addEdge(2,4);
//console.log(graph);
//console.log(graph.adj);
graph.showGraph();
document.write("<br/>");
document.write("======深度度优先搜索=====");
graph.dfs(0);
document.write("<br/>");
document.write("======广度优先搜索=====");
var graph1=new Graph(5);
graph1.addEdge(0,1);
graph1.addEdge(0,2);
graph1.addEdge(1,3);
graph1.addEdge(2,4);
graph1.bfs(0);
</script>
</body>
</html>
更多无权图的应用-application
flood fill
扫雷
走迷宫,迷宫生成, 迷宫的本质是一颗树 迷宫生成,是一个生成树的过程
欧拉路径
哈密尔路径
二分图
地图填色问题

